论文详情
Paper Details

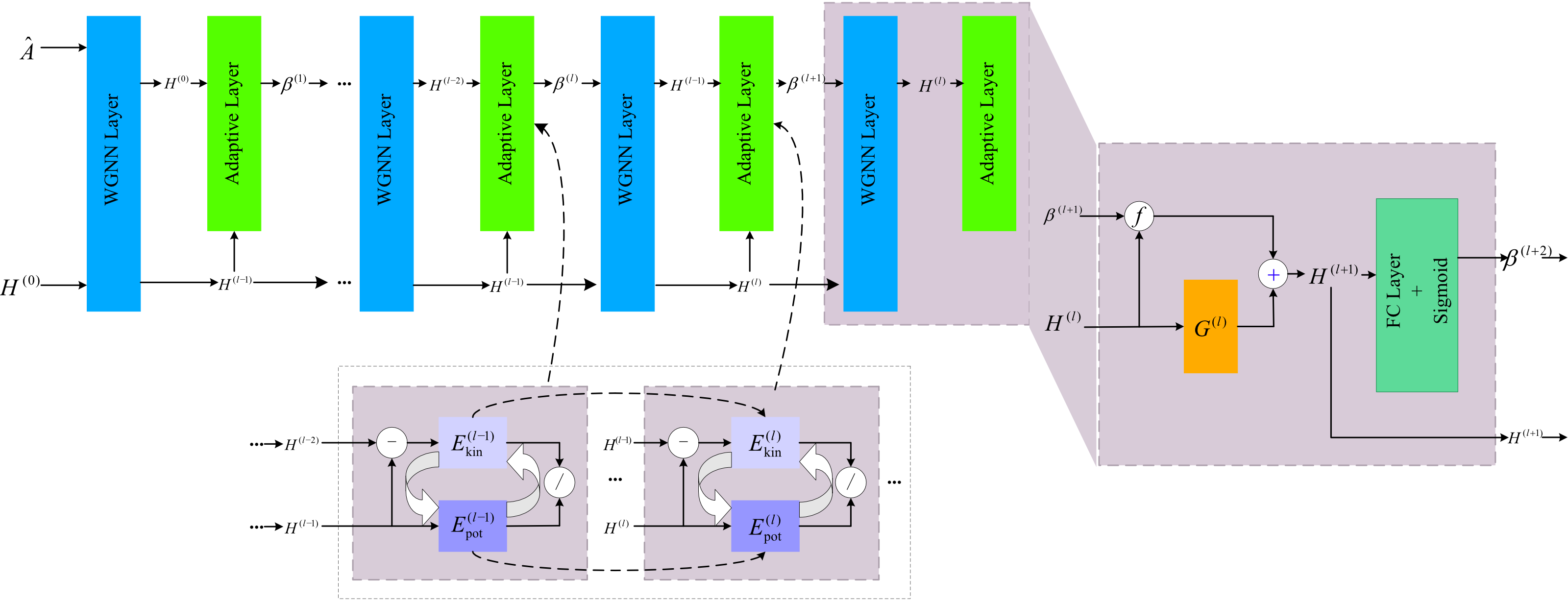
Over-smoothing is a persistent challenge in Graph Neural Networks (GNNs), where node embeddings become indistinguishable as network depth increases, fundamentally limiting their effectiveness on tasks requiring fine-grained distinctions. This issue arises from the reliance on diffusion-based propagation mechanisms, which suppress high-frequency information essential for preserving feature diversity. To mitigate this, we propose a wave-driven GNN framework that redefines feature propagation through the wave equation. Unlike diffusion, the wave equation incorporates second-order dynamics, balancing smoothing and oscillatory behavior to retain high-frequency components while ensuring effective information flow. To enhance the stability and convergence of wave equation discretization on graphs, an energy-based mechanism inspired by kinetic and potential energy dynamics is introduced, balancing temporal evolution and structural alignment to stabilize propagation. Extensive experiments on benchmark datasets, including Cora, Citeseer, and PubMed, as well as real-world graphs, demonstrate that the proposed framework achieves state-of-the-art performance, effectively mitigating over-smoothing and enabling deeper, more expressive architectures.